意地でも関心を分離する
マイクロサービスアーキテクチャにおいて、ある構造化されたデータを、構造を維持したまま別のコンポーネントでも使いたくなる誘惑が存在する。 例えば、ドメインロジックを扱うコンポーネントに「ユーザーの種別(ゲスト、メンバー、管理者)」という概念があり、API トークンの認可情報に含めたいとして、APIトークンを管理するコンポーネントはその概念に関与すべきだろうか。
// 関与しない定義 IssueToken(userType: string, expiresAt: Date): Token // 関与する定義 enum UserType { Guest, Member, Admin, } IssueToken(userType: UserType, expiresAt: Date): Token
ここで安易にそうしてしまうと、「ユーザーの種別」の定義が変わったとき——例えば新たに「モデレーター」という種別が追加された場合、双方のコンポーネント両方のデプロイが必要となってしまう。互換性を維持する手間や、対応漏れに起因するバグのリスクが生まれるため、マイクロサービスアーキテクチャの利点が損なわれる。
そのため、マイクロサービスアーキテクチャを採用する際は、上流のコンポーネントに依存した表現・挙動を可能な限り排除すべきだ。 Protobufなどのモジュールシステムを使えば同一のスキーマを複数のコンポーネントで使いまわすことができるが、やり過ぎればコンポーネント間のロジックの漏洩や共依存の温床となってしまう。データを他のコンポーネントに渡す時は、例えそれが構造化されたものであっても、任意の文字列とみなして扱うべき、くらいの勢いで考えていきたい。
リリースされていない変更が溜まるのを防ぐGitHub Action「tocenbough」
チームでソフトウェア開発をするとき、一度のリリースに含まれる変更が多すぎることにより、動作検証に時間がかかったり、問題が発生した時の原因特定が難しくなることがある。これを防ぐため、tocenboughというGitHub Actionを作った。読み方はもちろん「とおせんぼう」だ。
内容は至ってシンプルで、前回のlatest releaseからのマージコミットの数を計算し、その数が閾値を上回ったら落ちるというだけのスクリプトである。かなり単純なので、動作を把握するにはソースを見てもらったほうが早いかもしれない。
# GitHubから最新のリリースのタグを取得する。これがプルリクエストの数をカウントする起点となる latest=$(curl -H "Authorization: Bearer ${{ inputs.token }}" --silent \ "https://api.github.com/repos/${{ github.repository }}/releases/latest" | jq -r .tag_name) # まだリリースがひとつもない場合、原初のコミットハッシュを設定する if [ "$latest" == "null" ]; then latest=4b825dc642cb6eb9a060e54bf8d69288fbee4904 fi log="$(git log --merges --format="%an %s" "$latest..origin/${{ github.event.pull_request.base.ref }}")" # マージコミットの数を数える。ただし、[bot]がつくものは別にカウントする。 pr_count=$(echo "$log" | grep -v 'bot]' | wc -l | xargs) bot_count=$(echo "$log" | grep 'bot]' | wc -l | xargs) # PR数の定数倍 + botによる変更数からスコアを計算する score=$(( $pr_count * ${{ inputs.multiplier }} + $bot_count )) expr="Total weight of unreleased PRs since $latest: ${{ inputs.multiplier }} * $pr_count[PRs] + $bot_count[bot] = $score" # GITHUB_STEP_SUMMARYに結果を書き込む echo -e "### tocenbough\n" >> $GITHUB_STEP_SUMMARY if [ "$score" -gt "${{ inputs.threshold }}" ]; then echo "We have too many unreleased changes! $expr" >> $GITHUB_STEP_SUMMARY if [ ${{ contains(github.event.pull_request.labels.*.name, 'cram') }} == "false" ]; then exit 1 fi else echo "$expr" >> $GITHUB_STEP_SUMMARY fi
最後のステップで参照している $GITHUB_STEP_SUMMARY は、job summary *1のパスである。ここに任意の文字列を書き込むと、GitHub ActionのSummaryページに表示できる。

より実用性を高めるため、いくつかの工夫を施している。
工夫: botによる変更の重みを調整する
dependabotやrenovateによるPRは数が嵩みやすいため、人の手による変更と同じようにカウントしたくない場合がある。そのため、 multiplier というパラメータを設定することで、人の手によるPRの重みを調整できる。
工夫: 緊急時は制限を突破できる
「cram」という名前のラベルをPRにつけると、制限を上回っていたとしてもjobは成功する。急いで修正したいものがある場合は次のリリースにねじ込むことができる。
結果
HERP社内で最も活発なリポジトリで半年ほど運用してみた結果、リリースサイクルが目に見えて改善された(導入前の半年間に比べ、リリース間隔の平均は5.5日から4.2日、中央値は6日から3日になった)。

「変更をマージするために、まず溜まっている変更をリリースする」というインセンティブが、リリース作業自体はもちろん、プロセスの改善をも促すため、予想以上に効果がありそうだ。
リリースの頻度や粒度に悩みのあるチームはお試しあれ。.github/workflowsの下に以下のような設定を置くことで導入できる。
name: tocenbough on: pull_request: types: [opened, reopened, labeled, unlabeled] jobs: cd: runs-on: ubuntu-latest steps: - uses: fumieval/tocenbough@v0 with: token: ${{ secrets.GITHUB_TOKEN }} threshold: 10
SendGridのEvent WebHookを検証する
メール配信プラットフォームであるSendGridは、メールの到達状況などを、呼び出し元のアプリケーションにWebHookで伝えることができる。
アプリケーションがSendGridからリクエストを受け取るには、当然インターネットからアクセスできるようにする必要があるが、何の考えもなしに開放してはセキュリティ的に不安だ。しかしご安心を、SendGridにはWebHookにデジタル署名をつける機能がある。本稿ではその使い方を紹介する。
まず、Mail Settingsから、Signed Event Webhook Requestsという項目に入る。画面のボタンをクリックすると、Verification Keyが生成され、電子署名が有効になる。これは我々(HERP)のシステムで実際に運用している鍵である。

この設定をすると、以後のWebHookには、X-Twilio-Email-Event-Webhook-SignatureとX-Twilio-Email-Event-Webhook-Timestampの二つのHTTPヘッダーが付与される。アプリケーション側はこれらを使って検証すればよい。
まず、電子署名に使うアルゴリズム、ハッシュ関数、メッセージ、署名、公開鍵を整理する。
- アルゴリズム: ECDSA(有限体上の楕円曲線がなす群構造を用いた電子署名アルゴリズム)
- ハッシュ関数: SHA256
- メッセージ:
X-Twilio-Email-Event-Webhook-Timestampの値と、リクエストボディを結合したもの - 署名:
X-Twilio-Email-Event-Webhook-Signature - 公開鍵:
Verification Key - 秘密鍵: SendGridが保有する
関係を整理したところで、公式のドキュメントを参考に実装を進めていく。docs.sendgrid.com
まずは必要なモジュールをインポートしていく。ずらずらと並べられた文は、もはやHaskellの風物詩である。
import "asn1-encoding" Data.ASN1.BinaryEncoding (BER(..)) import "asn1-encoding" Data.ASN1.Encoding (decodeASN1) import "asn1-types" Data.ASN1.Types (ASN1(..), fromASN1) import "base" Data.Proxy import "base" Data.Bifunctor (bimap, first) import "base64" Data.ByteString.Base64 (decodeBase64) import "bytestring" Data.ByteString qualified as B import "bytestring" Data.ByteString.Lazy qualified as BL import "cryptonite" Crypto.ECC (Curve_P256R1) import "cryptonite" Crypto.Error (CryptoFailable(..)) import "cryptonite" Crypto.Hash.Algorithms (SHA256(..)) import "cryptonite" Crypto.PubKey.ECC.Types (CurveName(..)) import "cryptonite" Crypto.PubKey.ECDSA qualified as ECDSA import "x509" Data.X509 (PubKey(..), PubKeyEC(..), SerializedPoint(..))
公開鍵がBase64とASN.1でエンコードされていることはすぐにわかるが、その中身のフォーマットがドキュメントに書かれていなかったため、少々迷いが生じた。実験してみたところx509パッケージのPubKeyとしてデコードできることがわかった。
type PublicKey = ECDSA.PublicKey Curve_P256R1 curve :: Proxy Curve_P256R1 curve = Proxy parsePublicKey :: B.ByteString -> Either String PublicKey parsePublicKey b64 = do -- base64としてデコード raw <- first show $ decodeBase64 b64 -- ASN.1としてデコード asn1 <- first show $ decodeASN1 BER $ BL.fromStrict raw -- 楕円曲線のパラメータのプリセットと、公開鍵を取り出す pubkey <- bimap show fst $ fromASN1 asn1 -- secp256r1と仮定する SerializedPoint point <- case pubkey of PubKeyEC (PubKeyEC_Named SEC_p256r1 bs) -> Right bs _ -> Left $ "Unsupported public key: " <> show pubkey -- 座標をデコード case ECDSA.decodePublic curve point of CryptoPassed a -> Right a CryptoFailed err -> Left $ show err
ここまで来れば、あとは関数を呼び出すだけなので簡単だ。暗号や電子署名は、実装を間違えればただのランダムな文字列になってしまうため、ライブラリのありがたみを感じやすい。
verify :: PublicKey -> B.ByteString -> B.ByteString -> B.ByteString -> Either String () verify pubKey timestamp payload signatureBase64 = do -- 署名をデコードする signature <- either (const $ Left "Malformed signature") pure $ decodeBase64 signatureBase64 -- ECDSAの署名(r, s)を取り出す point <- case decodeASN1 BER $ BL.fromStrict signature of Right [_, IntVal r, IntVal s, _] -> pure (r, s) Right asn1 -> Left $ "failed to decode the signature: " <> show asn1 Left err -> Left $ show err case ECDSA.signatureFromIntegers curve point of CryptoPassed sig | ECDSA.verify -- 検証する curve SHA256 pubKey sig $ timestamp <> payload -> pure () | otherwise -> Left "Verification failed" CryptoFailed _ -> Left "ECDSA.signatureFromIntegers failed"
WebHookの設定画面で「Test Your Integration」をクリックすると送られてくるデータを使って、実際に検証してみる。
_test_verify :: Either String ()
_test_verify = do
pub <- parsePublicKey "MFkwEwYHKoZIzj0CAQYIKoZIzj0DAQcDQgAERYcga9cTuvv0EbOFM0PO/KJjCgqYwtGar22uUyPQPwUbm+OtKXGNGIaHBvkgXBCbTxG4XQ4ddfDPgfMAcguUtg=="
verify pub
"1655455728"
"[{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"processed\",\"category\":[\"cat facts\"],\"sg_event_id\":\"cPeOfuc93o3vAEftXKt_zA==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"deferred\",\"category\":[\"cat facts\"],\"sg_event_id\":\"zFYYFn__N8lr3be4TqKnVw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"response\":\"400 try again later\",\"attempt\":\"5\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"delivered\",\"category\":[\"cat facts\"],\"sg_event_id\":\"rj8WvpmTWgE0z2MSd41KKg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"response\":\"250 OK\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"open\",\"category\":[\"cat facts\"],\"sg_event_id\":\"uz1AaVpvYihASovU-M-Jrg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"click\",\"category\":[\"cat facts\"],\"sg_event_id\":\"O2bZwfxc-xm-9zmeVZX8HA==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"bounce\",\"category\":[\"cat facts\"],\"sg_event_id\":\"vMLN27M1-TVv5XADvpW3Nw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"reason\":\"500 unknown recipient\",\"status\":\"5.0.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"dropped\",\"category\":[\"cat facts\"],\"sg_event_id\":\"u1u9xdYlTkoDkUZFZ_j_tg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"reason\":\"Bounced Address\",\"status\":\"5.0.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"spamreport\",\"category\":[\"cat facts\"],\"sg_event_id\":\"CjkStOi15hPQfWO58rH9dw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"unsubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"QrCQiwv2pfkejKE5Zi1D0g==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"group_unsubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"l67dvY6MIupGpuk1r9vIXw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\",\"asm_group_id\":10},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"group_resubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"fo7PLpVCoCA9WDHovGQyyw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\",\"asm_group_id\":10}]\r\n"
"MEUCIQCBYJiC1zzZeM61EbekWSGMFgpRSzaQSA4zwV3vlMgf/wIgSrMZIIYTnx4dkqDK92re4WYhcM3xEKbLIKfmcu7Et0o="
_test_verify_fail :: Either String ()
_test_verify_fail = do
pub <- parsePublicKey "MFkwEwYHKoZIzj0CAQYIKoZIzj0DAQcDQgAERYcga9cTuvv0EbOFM0PO/KJjCgqYwtGar22uUyPQPwUbm+OtKXGNGIaHBvkgXBCbTxG4XQ4ddfDPgfMAcguUtg=="
verify pub
"1655455729"
"[{\"email\":\"bob@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"processed\",\"category\":[\"cat facts\"],\"sg_event_id\":\"cPeOfuc93o3vAEftXKt_zA==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"deferred\",\"category\":[\"cat facts\"],\"sg_event_id\":\"zFYYFn__N8lr3be4TqKnVw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"response\":\"400 try again later\",\"attempt\":\"5\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"delivered\",\"category\":[\"cat facts\"],\"sg_event_id\":\"rj8WvpmTWgE0z2MSd41KKg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"response\":\"250 OK\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"open\",\"category\":[\"cat facts\"],\"sg_event_id\":\"uz1AaVpvYihASovU-M-Jrg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"click\",\"category\":[\"cat facts\"],\"sg_event_id\":\"O2bZwfxc-xm-9zmeVZX8HA==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"bounce\",\"category\":[\"cat facts\"],\"sg_event_id\":\"vMLN27M1-TVv5XADvpW3Nw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"reason\":\"500 unknown recipient\",\"status\":\"5.0.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"dropped\",\"category\":[\"cat facts\"],\"sg_event_id\":\"u1u9xdYlTkoDkUZFZ_j_tg==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"reason\":\"Bounced Address\",\"status\":\"5.0.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"spamreport\",\"category\":[\"cat facts\"],\"sg_event_id\":\"CjkStOi15hPQfWO58rH9dw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"unsubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"QrCQiwv2pfkejKE5Zi1D0g==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\"},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"group_unsubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"l67dvY6MIupGpuk1r9vIXw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\",\"asm_group_id\":10},\r\n{\"email\":\"example@test.com\",\"timestamp\":1655455223,\"smtp-id\":\"\\u003c14c5d75ce93.dfd.64b469@ismtpd-555\\u003e\",\"event\":\"group_resubscribe\",\"category\":[\"cat facts\"],\"sg_event_id\":\"fo7PLpVCoCA9WDHovGQyyw==\",\"sg_message_id\":\"14c5d75ce93.dfd.64b469.filter0001.16648.5515E0B88.0\",\"useragent\":\"Mozilla/4.0 (compatible; MSIE 6.1; Windows XP; .NET CLR 1.1.4322; .NET CLR 2.0.50727)\",\"ip\":\"255.255.255.255\",\"url\":\"http://www.sendgrid.com/\",\"asm_group_id\":10}]\r\n"
"MEUCIQCBYJiC1zzZeM61EbekWSGMFgpRSzaQSA4zwV3vlMgf/wIgSrMZIIYTnx4dkqDK92re4WYhcM3xEKbLIKfmcu7Et0o="
ghci> _test_verify Right () ghci> _test_verify_fail Left "Verification failed"
SendGridから送られてきたデータは通り、改ざんしたデータは弾けることを確認できた。
まとめ
インターネットサバンナの住人として、不正な情報に対する警戒は怠ってはいけない。SendGridは「リクエストの内容とタイムスタンプをECDSAで署名する」というシンプルな仕組みがあるおかげで、比較的少ないコードで検証機能を実装できた。
PR枠
WebHookの門はECDSAによって閉ざされているが、採用においてHERPの門は開かれている。HERPは頭が良くて物事を成し遂げられる人を募集しています。
依存関係と階層構造の軛
21世紀現在のプログラミング言語において、モジュールという機能はほぼ必要不可欠である。ソースコードを分割し、明示的な依存関係を指定する仕組みであるモジュールは、以下のような様々な恩恵をもたらす。
- インクリメンタルビルド: モジュールごとにコンパイル結果を保存し、変更されていない部分を再コンパイルするのを防ぐ。
- 内部の隠蔽: 実装の詳細を隠蔽し、モジュール外から触れないようにする。プログラムの見通しをよくしたり、不正な操作をする機会を減らす。
- アーキテクチャの整理: モジュールは他のモジュールを参照できるが、原則として相互参照はしない。依存の向きを定めることで、適切な抽象化と、 それに基づいた実装の分離を促す。
さて、いくらモジュールが便利と言えど、数が増えすぎるとさすがに扱いにくい*1。そのため、ディレクトリの構造をモジュールの階層構造として運用する仕組みが備わっていることが多い。 コンパイラから見れば、ドットなどで区切られたモジュール名から、対応するファイルを探すだけの話だ。あくまで人間の都合であり、上で挙げたような恩恵とはあまり関係してこない──だが、本当にそれでいいのだろうか。
若干わざとらしい例ではあるが、掲示板のアプリケーションを実装するに当たり、以下のようにモジュールを分割するとしよう。
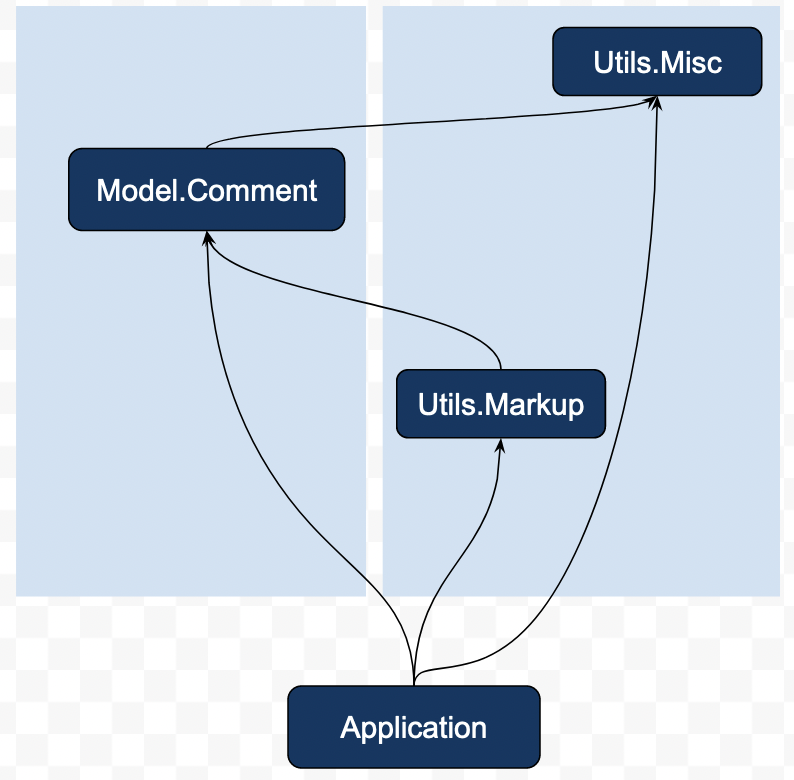
UtilsとModelの二つのディレクトリを設ける。Model.Commentでは、投稿を表すデータ型や、データベースの操作を定義する。Utils.Miscには雑多な便利関数をまとめ、Utils.Markupでは、投稿をHTMLに変換する処理を記述する。
あからさまかもしれないがこの構造には問題がある。というのも、UtilsとModelsは、ディレクトリ単位で見ると、双方向に依存関係を持っているのだ。 先述した通り、コンパイラから見れば、モジュールがどこのディレクトリに属していようが本質は変わらないし、正しい入力である。しかし、開発者はディレクトリの分割に意味を見出しているという齟齬が発生する(そして、コンパイラはそれを指摘しようがない)。この齟齬を放置したまま開発を続けていくと、想定外に深い依存関係が発生してビルドが遅くなったり、「Modelに依存したUtils」という存在と辻褄を合わせるために、本来隠蔽すべき詳細がどんどん漏れ出したりしてしまう。
これを防ぐ手段として、それぞれのディレクトリをパッケージ化し、依存関係を明示するというものがある。これは双方向の依存を防ぐという意味では効果的な一方、パッケージごとのメタデータを管理するコストが高まったり、パッケージ単位でのキャッシュはできても、モジュール単位のインクリメンタルビルドが効きにくくなるなど、デメリットも無視できない。
ならば、新たに静的解析を実装し、こういった問題を検出しようではないか。まずはモジュールの依存関係のグラフを可視化して見通しを立てたい──dot形式に変換し、graphvizで表示するだけの簡単な話だ。

……どうやら、そんな簡単な話ではなかったようだ。
もう少し、ディレクトリ同士の依存関係に着目して考えてみよう。Foo.Bar.A.BがFoo.Baz.C.Dに依存しているとき、「BarがBazに依存している」という情報さえ残せば、それより深い部分の情報は削いでも構わない。つまり、以下のようなアルゴリズムでグラフを導き出す。
- 依存元、依存先のモジュール名をドットで区切り、リストにする
- どちらかのリストが空になったら、終了する
- リストの先頭を見る
- 名前が同じなら、先頭を取り除く
- 名前が違っていたら、辺を作成する
「Foo.BarがFoo.Bar.Bazに依存している」のような関係は今回は考慮しない。もし考慮したい場合は、「リストが空になったら、辺を作成する」ように書き換えればよい。
このアルゴリズムを利用すると、親のディレクトリごとに分割されたグラフができ、graphvizのcircoを使うと図のようになる。最初のグラフとはえらい違いだ。
巨大なコードベースにおけるモジュール間の依存関係は、愚直に描画したところでスパゲッティどころではない度し難いモノにしかならない。そこで、階層ごとに依存関係を「割る」──すなわち、モジュールをまとめたフォルダ同士にも依存関係を見出し、再帰的に要約することによって、美しく可視化できた pic.twitter.com/dwx3MA2DCH
— ふみ a.k.a.DJ Monad (@fumieval) 2022年4月28日
成分をクローズアップすると以下のようになる。ディレクトリに要約されているため、関係が読みやすくなっているのがわかる。
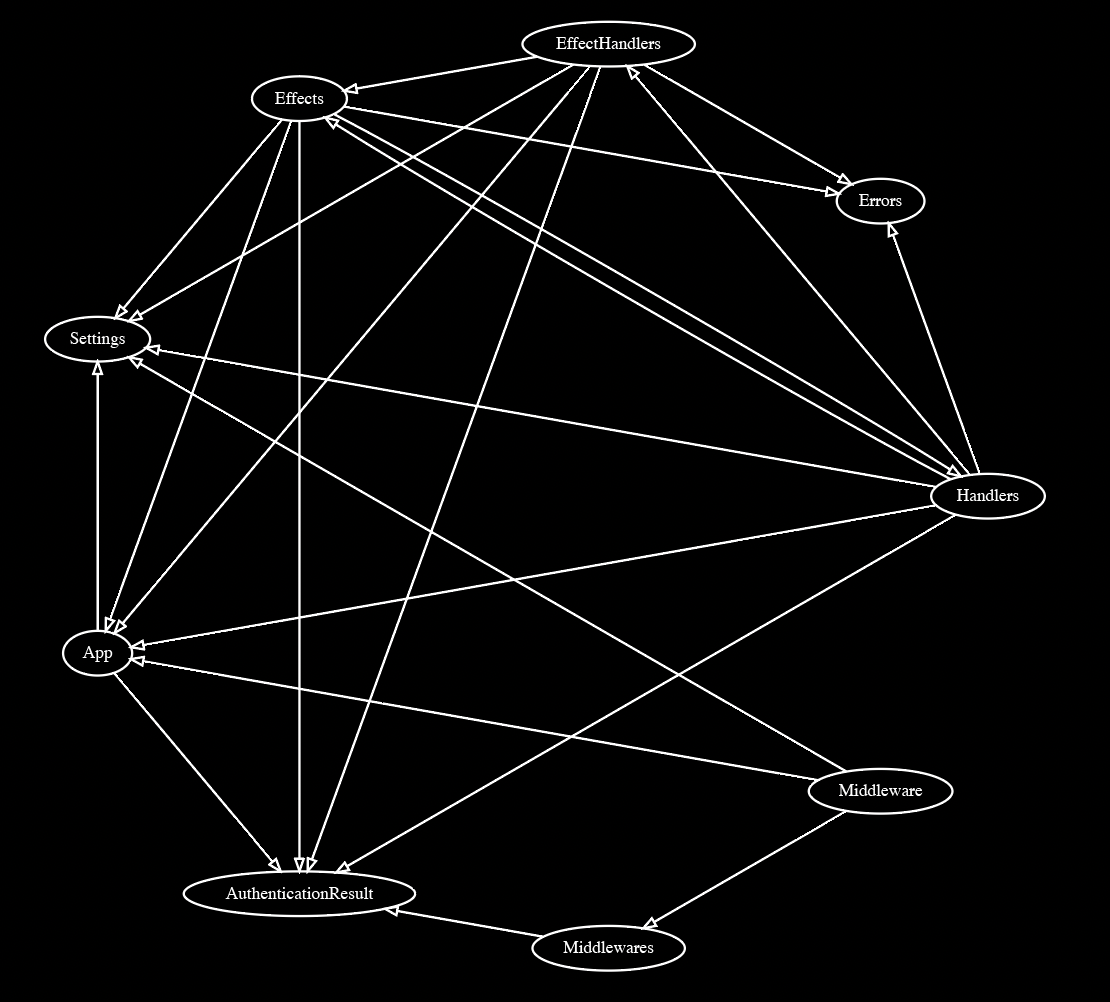
だが本題に戻ろう。ディレクトリの意義を保つためには、相互依存がない──いや、さらに有向閉路が存在しないことを保証したい。つまり、強連結成分分解すればよいのだ。早速会社のコードベースに適用してみると、かなりの大物が釣れた。各辺の重みはインポートの件数を表す。
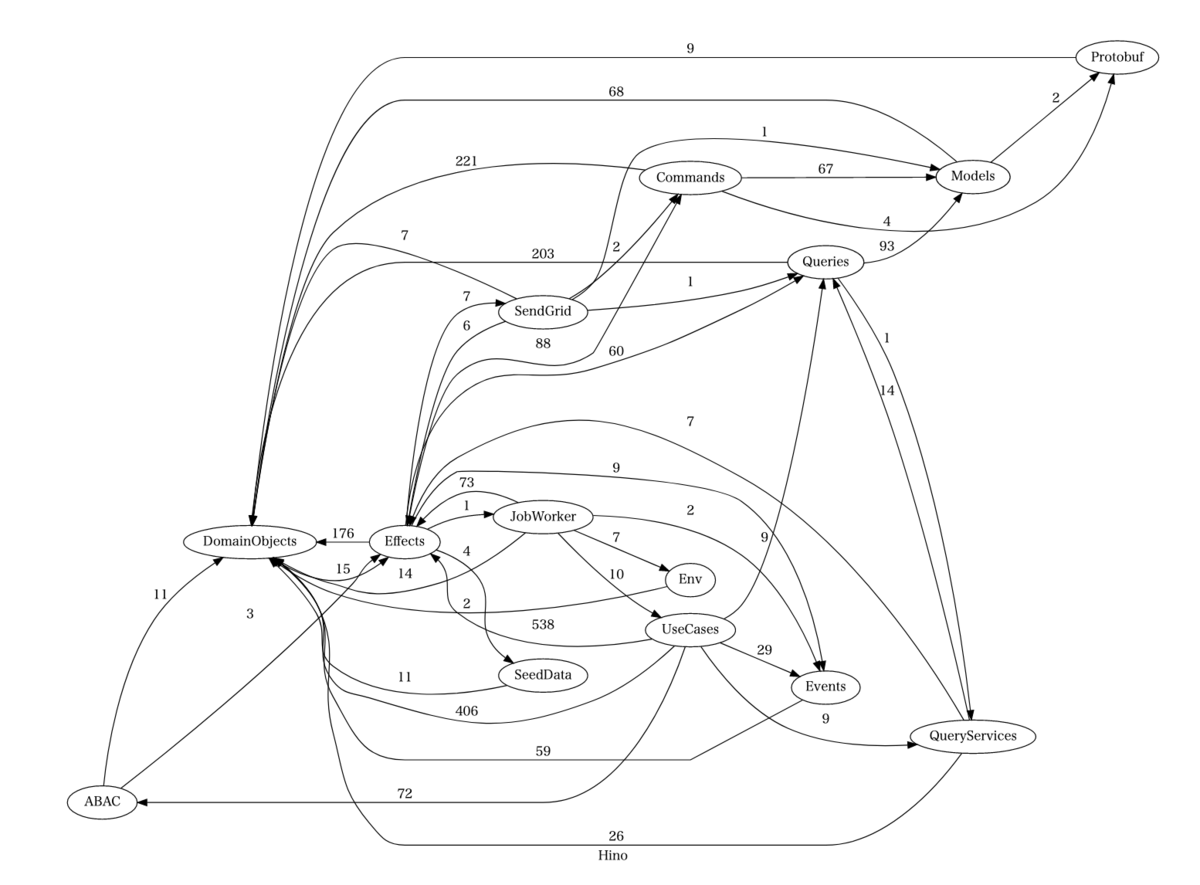
このグラフは強連結であり、すなわちどの頂点の間にも道が存在する。本来、このようなことが発生しないようにパッケージを分割していたはずなので少々驚きの結果だ。パッケージが細かすぎたゆえに、抜け道ができてしまったのだろう。
有向非巡回グラフにするために取り除くべき辺はFeedback arc set(FAS)と呼ばれている。 最小のFASを求めるのはNP困難だが、今回のケースでは抜け道の重みが圧倒的に小さい。そのため、重い辺から順に再構築していき、閉路を生む候補だけ弾く貪欲法で実用的な結果が得られそうだ。
件のグラフについては、以下の四つを除去するとDAGになる。幸い、件数はそれほど多くないので、循環をなくすのはそれほど難しくなさそうだ。
Queries -> QueryServices Effects -> JobWorker SendGrid -> Effects DomainObjects -> Effects
ここまでの処理を自動化するため、Haskellコンパイラのプラグインとして実装したスタンドアロンのコマンドラインツールとして実装した。 orderorder srcを実行すると、src以下のモジュール同士の依存関係を調べ、強連結成分を列挙する。この結果を保存しておいて差分をCIなどでチェックすれば、関係を破壊するような依存関係が増えた際に気付くことが可能になる。
もちろん、ここまでの議論はHaskell以外にも適用できるため、他の言語にも同等のものを実装することは可能なはずだ。
まとめ
今まではモジュールの階層構造に明確なルールがなく、ある意味飾りだった。しかし「ディレクトリ間の依存関係」という概念を導入することで、自然に「モジュールの依存関係がDAGであるように、ディレクトリの依存関係もまたDAGになる」という制約を導入でき、我々の直観とのすり合わせができた。この仕組みをクリーンアーキテクチャの促進・保守に活用していきたい。
PR枠
ここまで散々階層構造の話をしてきたが、HERPはオープンでフラットな組織を是としており、現在も積極的に技術者を募集している。興味のある方は、以下の資料を参照されたし。
株式会社HERPに転職しました
GitHubのプロフィールを見た人などはもしかしたら気づいているかもしれないが、Tsuru Capital LLCを退職し、2022年2月16日よりHERPの正社員となった。HERPは、大まかに言えば採用活動を管理するプラットフォームを提供している。
きっかけ
Tsuru CapitalはKospi(韓国株のインデックス)のデリバティブを半自動取引する企業で、Haskellを使っているというのが最大の特徴として知られる謎多き会社だ。2015年に入社し、2022年まで6年以上働いた。流石に同じ職場にずっといると経験が偏ってしまうし、感覚としても飽きがきたので転職を考えた。 また、ある時期からRustメインの開発をするようになったが、やはり自分の最大の強みであるHaskellを活かせる仕事をしたく、転職先を考える基準となった。 拙作のライブラリであるextensibleを使っているという情報もあったため、偵察がてらHERPに応募した。
入社までの流れ
採用プロセスを扱う企業なだけあってかなり迅速で、体験が良かった。
- 2021/12/14: ウェブサイトから応募
- 2021/12/15: カジュアル面談
- 2021/12/16: 一次面接(構造化面接、事前のアンケートで答えた内容をもとに、前職の成果などについて話した)
- 2021/12/21: 二次面接(価値観が適合するかどうかを、カジュアルな会話で確認した)
- 2021/12/28: オファー面談
並行してリファレンスチェックを行った(上司、同僚、部下1名ずつを希望されたが、基本的に階層構造がない組織なので自分の裁量で3人選んだ)。
あまりにもスムーズというか、こちらが一方的に有利なように感じられたので、もう少し試して欲しかった気もする。だが、HERPの文化と自社の製品がなす候補者体験は確実に強みと言える。
現在
コードベースの品質を改善したり、新機能を実装したり、洗い物をしたりと自主的に色々なことをやっている。自分のスキルについて極端な不足や過剰を感じることはなく、コミュニケーションも盛んなため、面白い課題は尽きず、楽しくやっていけそうだと思う。開発者チームは適度にオタク性と社会性があり、キラキラしすぎていないところも好感を持てた。
かなり高い期待を受けて入社したので、それに応えるように成果を出していきたい。
リンク
Oath: 安全、高速、合成可能な並行処理
TL;DR
並行処理を簡潔かつ安全に記述できるライブラリを作った。ApplicativeDo拡張を使って、以下のようにoathの引数として与えたIOアクションを同時に実行し、結果を集める処理を書ける。いずれかが例外を投げた場合、残りをキャンセルするためリソースを漏らす心配がない。
evalOath $ do a <- oath $ ... b <- oath $ ... f a b
経緯
Haskellは並行処理が得意とされている。事実、軽量スレッド、MVar、STMといった処理系によるサポートが充実しており、HackageのConcurrencyカテゴリには235ものパッケージがあることからもユーザの関心の高さが窺える。 並行処理を実用する上では、単にスレッドをフォークするだけでなく、計算の結果を集める必要がある──Scalaなどで言うFutureに近いものがあると嬉しい。案の定、並行計算の結果を取り出すためのHaskellライブラリは数多く作られてきた。
futuresというなかなかいい名前のパッケージがある。APIもかなりシンプルだ。 スレッドをフォークして、計算結果をMVarに代入し、MVarの中身を取り出すアクションを返すというものだ。
fork :: IO a -> IO (Future a) fork io = do mv <- newEmptyMVar forkIO $ do a <- io putMVar mv a return $ Future $ readMVar mv
考え方はわかりやすいが、この実装には致命的な欠点がある──例外処理である。forkに与えたアクションが例外を発生させても、誰も対応ができない。しかも、putMVarが呼ばれなくなるのでreadMVarが発散してしまう(実行時エラーになる)。これでは実用するのは難しい。また、forkIOの結果であるThreadIdが捨てられていることからわかるように、一度始めた計算を外部から止めるすべはない。
spawnは、Future型ではなく直接IOを返す点を除けばfuturesと似ている。
spawnTry :: IO a -> IO (IO (Result a)) spawnTry m = do v <- newEmptyMVar _ <- mask $ \restore -> forkIO (try (restore m) >>= putMVar v) return (readMVar v) spawn :: IO a -> IO (IO a) spawn m = do r <- spawnTry m return (r >>= either throwIO return)
こちらはきちんと例外処理をしており、putMVarが呼ばれることが保証されるためいくらか実用的だ。しかし、やはり計算は止められない。
promiseは、ApplicativeとMonadのインスタンスであるPromise型が売りだ。
newtype Promise a = Promise { unPromise :: IO (Async a) } deriving (Functor) instance Applicative Promise where pure = Promise . async . return Promise mf <*> Promise mx = Promise $ do f <- mf x <- mx (f', x') <- waitBoth f x async $ return $ f' x' instance Monad Promise where return = liftIO . return Promise m >>= f = Promise $ m >>= wait >>= unPromise . f liftIO :: IO a -> Promise a liftIO = Promise . async
外側のIOでスレッドをフォークし、内側のAsyncで結果を待つという仕組みのようだ。だが、m <*> nはmとnをそれぞれ並行して実行したのち、両方の結果が返ってくるのをその場で待つ必要がある(「待つAsyncを返す」のではなく、「待ってからAsyncを返す」)。これでは(a *> b) *> cとa *> (b *> c)の挙動が異なってしまうため、Applicativeの則を満たさない。また、Asyncは本来cancel`できるはずだが、合成中に結果を待ってしまうので事実上中断ができない(どちらにせよ、Promiseの実装が隠蔽されているのでどうしようもないが)。
さらに、Monadは左の計算の結果を待ってから右に進むという挙動で、Applicativeとの一貫性がない。いくらインスタンスがあっても、これでプログラムを組み立てるのは難しいだろう。
非同期処理の定番であるasyncパッケージには、Concurrentlyという型がある。
newtype Concurrently a = Concurrently { runConcurrently :: IO a } instance Applicative Concurrently where pure = Concurrently . return Concurrently fs <*> Concurrently as = Concurrently $ (\(f, a) -> f a) <$> concurrently fs as instance Alternative Concurrently where empty = Concurrently $ forever (threadDelay maxBound) Concurrently as <|> Concurrently bs = Concurrently $ either id id <$> race as bs
(<*>)はconcurrently :: IO a -> IO b -> IO (a, b)を使って両方の結果を待つ計算を表現し、(<|>)はrace :: IO a -> IO b -> IO (Either a b)はどちらかが返ってくるまで待つ計算を表現する。promiseと違い、その場で待機する必要がないので、Applicative則を満たしそうだ。
concurrentlyおよびraceは、スレッドを必ず二つフォークする上、かなり複雑な実装なので、オーバーヘッドが大きそうだ。ここまで見た中では一番正しそうで使いやすそうな実装だが、もっといい方法はないだろうか。
継続とSTMのコンボ
非同期処理を安全に合成する方法には覚えがある。単純で頑強なメッセージングシステム、franz - モナドとわたしとコモナドで紹介した、継続渡しを用いて結果を待つトランザクションを渡すという仕組みだ。この方法なら、継続が終了したタイミングで処理を中断できるため、待つもやめるも自由自在、リソースの解放漏れの心配はない(franzはこのメカニズムによって非同期リクエストを管理している)。そのエッセンスを独立したライブラリに蒸留できそうだ。それっぽい名前はだいたい取られていたので、Promiseからの連想でOathと名付けた。
newtype Oath a = Oath { runOath :: forall r. (STM a -> IO r) -> IO r } deriving Functor instance Applicative Oath where pure a = Oath $ \cont -> cont (pure a) Oath m <*> Oath n = Oath $ \cont -> m $ \f -> n $ \x -> cont (f <*> x)
Oathは、IO (STM a)をCPS変換したもので、Compose (Codensity IO) STMと等価である*1 *2。外側のIOで計算を起動し、内側のSTMで結果を待つ。OathはApplicativeインスタンスを持ち、STM (a -> b)とSTM aを用意してから、それらを合成したSTM bを返す――計算の起動と、結果の待機を別々に合成するというわけだ。
oath :: IO a -> Oath a oath act = Oath $ \cont -> do v <- newEmptyTMVarIO tid <- forkFinally act (atomically . putTMVar v) let await = readTMVar v >>= either throwSTM pure cont await `finally` killThread tid
oathは、IOアクションを別のスレッドで実行し、その結果をTMVar経由で取り出す。forkFinallyが例外を受け止め、throwSTMがそれを伝える。
生殺与奪の権は継続が握っており、終了したときにThreadKilled例外が投げられる。このような挙動をwithAsyncなどで安全に表現しようとすると、withAsync foo $ \a -> withAsync bar $ \b -> ...のように
ネストが深くなってしまいがちだが、Oathは継続渡しの抽象化によって、combine <$> oathSTM foo <*> oathSTM barのようにフラットに書ける。それだけでなく、traverseでコンテナに対しても簡単に適用できるという利点もある。
Oathを実行するには、単にevalOathを呼び出す。もちろん、結果を待つタイミングを制御したい場合はrunOathを直接呼ぶべき場面もあるだろう。
evalOath :: Oath a -> IO a evalOath m = runOath m atomically
Alternativeの<|>は、Concurrentlyと同様両方の計算を起動するが、一方が完了した段階でもう片方はキャンセルする(STMのAlternativeインスタンスを継承している)。
Control.Concurrent.STM.Delayのラッパーも提供しており、<|>で合成するだけで、タイムアウト処理を非常に簡単に記述できる。
また、「リソースの確保」「解放」「使用」という三つの挙動を一つにまとめられるという継続渡しの強みがdelayの実装によく表れている。
instance Alternative Oath where empty = Oath $ \cont -> cont empty Oath m <|> Oath n = Oath $ \cont -> m $ \a -> n $ \b -> cont (a <|> b) delay :: Int -> Oath () delay dur = Oath $ \cont -> bracket (newDelay dur) cancelDelay (cont . waitDelay)
Concurrentlyと違い、Oathはフォークは必須ではないのもポイントだ。例えばネットワーク経由でリクエストを送信する処理は書いた順序で実行し、結果を待つ部分だけ非同期にするといった実装もできる。forkOnなど、forkIO以外のフォークも使えるため自由度が高く、そもそもフォークしないという選択肢もあるため、決定性が求められる単体テストの実装などにも役に立つだろう。
パフォーマンス
最後に、Concurrentlyと比較するためのベンチマークを行った。他のパッケージはまともに動作しないため、評価の対象から外した(単体テストは残してある)。
, bench "oath STM 100" $ nfIO $ O.evalOath $ traverse (O.oath . pure) [0 :: Int ..99] , bench "async 100" $ nfIO $ A.runConcurrently $ traverse (A.Concurrently . pure) [0 :: Int ..99]
oath IO 10: OK (0.86s)
3.18 μs ± 206 ns
oath STM 10: OK (0.34s)
5.10 μs ± 169 ns
async 10: OK (0.66s)
10.0 μs ± 190 ns
oath IO 100: OK (0.60s)
35.8 μs ± 2.4 μs
oath STM 100: OK (0.39s)
48.0 μs ± 1.3 μs
async 100: OK (0.21s)
100 μs ± 5.6 μs
オーバーヘッドはConcurrentlyの約半分に抑えられている。Concurrentlyは(<*>)の左右ごとにスレッドをフォークするため、項の二倍フォークする必要があるという点が表れているのだろう。
まとめ
Oathは、継続渡しスタイルとSTMを組み合わせることによって、柔軟、安全、高速、そして合成可能な非同期処理の表現を可能にした。単にIOアクションを組み立てる道具としても便利だが、今後はOathに基づいたAPIデザインにも一考の余地があると考えている。並行処理の新定番を狙っていきたい。
新しいGHC拡張、NoFieldSelectorsについて
今まで不満の多かったHaskellのレコードの扱いを改善するための一歩として、NoFieldSelectorsというGHC拡張の実装を進めている。
動機
Haskellにはレコードを定義するための構文がある。
data User = User { userId :: Int , userName :: Text }
こう定義すると、各フィールドごとにuserId :: User -> IntとuserName :: User -> Textというゲッターに相当する関数が生成される。これらの関数は特別な意味合いを持っており、以下のレコード操作の構文にも利用できる。
- 構築
User { userId = 0, userName = "Zero" } - パターンマッチ
case foo of User { userId = x, userName = name } -> ... - 更新
foo { userId = 1 }
しかし、フィールドと同じ名前の関数こそが使いづらさの原因となっている。
多くのプログラミング言語では、構造体のフィールドはそれぞれ固有の名前空間に属するが、Haskellはそうではない。以下のような定義は、idがUserなのかArticleなのか、それともPreludeのid :: a -> aなのか判別できないため、実際には使えない。
data User = User { id :: Int, name :: Text } data Article = Article { id :: Int, title :: Text }
そのため、userId、articleIdのように型名を接頭辞にするのが通例となっている。
するとタイプ数が増えるばかりか、JSONなどのフォーマットに変換する際に接頭辞を切り取るための仕組みなども必要になり、使い勝手がよくない。lensや拡張可能レコードなどの技法で改善できる面もあるものの、RecordWildCardsやNamedFieldPunsなどの構文的な支援や、網羅性のチェックが受けられなくなるのは痛い。
DuplicateRecordFields拡張を用いれば、複数のデータ型で同じフィールド名を採用することも一応許される。しかし、ゲッター関数がどのデータ型に属するか判定するためのマジカルな実装があり、進んで使いたいものではないのが実情である(そのハックを無くす提案が最近受理された *1 )。
忘れがちだが、複数のコンストラクタを持つデータ型においてもレコードの構文は使える。その場合、対応するコンストラクタ以外にはエラーを出す部分関数が生成されるため大変使い勝手が悪く、実質的にないものとして扱われている。
提案
そんな問題を解決するアプローチとして、NoFieldSelectorsという拡張が提案された。
この拡張を有効にすると、レコードを定義しても、ゲッター関数としては使えなくなるが、レコードの構文としては使える――つまり、短い名前のデメリット(コンフリクト)をなくし、メリット(簡潔なコード)だけを得られるというわけだ。DuplicateRecordFieldsと併用すれば、複数のデータ型で同じフィールド名を気兼ねなく定義できる。
目の上のたんこぶだったゲッター関数の問題を回避できれば、他の言語と遜色ないレコード操作が可能になり、レコード自体の採用率も高まることが予想される。 プレーンなデータ型で起きがちな、変更に伴う破壊や、値の順番を間違えるバグを回避しやすくなり、Haskellの強みの一つであるジェネリクスを使った導出機構を活用できる場面も増える。
さらに、いずれ実装されるであろうRecordDotSyntax(プロポーザル, 日本語の紹介スライド)の実用性を飛躍的に高めるだろう。
要約すると、NoFieldSelectorsは以下のメリットをもたらす。
- フィールド名に接頭辞を付けなくてよくなる
instance FromJSON Fooのように、そのままインスタンスを導出できる場面が増える- 今までは単なるバッドプラクティスだった、複数コンストラクタのレコードが実用的になる
- 害を及ぼす心配なくレコードを導入できる
実装
提案者のSimon Hafner氏により、フラグの追加や試験的な実装が作られ、私が実際に機能する段階まであらかた完成させた。現在はレビュー段階にある。
Implement NoFieldSelectors (!4017) · Merge Requests · Glasgow Haskell Compiler / GHC · GitLab
単に関数の生成をやめればいいかと思いきや、そこまで単純な話ではなかったようだ。各種レコード操作をコンパイルするときの振る舞いは、ゲッター関数の存在を前提としている。それを省いてしまうと、単なるレコードでないデータ型と同じになってしまうのだ。フィールドに相当するシンボルは今まで通り作られるが、項としてコンパイルするときはそれを隠す、というアプローチをとった。この辺りは、DuplicateRecordFieldsなどの機能との兼ね合いで泥臭いものとなったが、Adam Gundry氏の助言のおかげで実装まで持っていくことができた。
このブランチはGHC 9.2までにはマージできるようにしたい。NoFieldSelectorsは、今まで避けようのなかった慣習を覆す機能であり、これが広まればGHC/Haskellという言語の全体像が変わるに違いない。まだ捕らぬ狸の皮算用でしかないが、GHCのレコードの進化を楽しみにしていただきたい。
2021/02/17 追記 Adam Gundry氏がGHCのレコード周りの内部仕様をブラッシュアップしたため、実装をリベースして再投稿していただいた。そしてついに16日、masterにマージされた。
将来
PolyKindsやStrictDataと同様、NoFieldSelectorsはモジュール単位でしか振る舞いを制御できない。将来的には、データ型単位で挙動をコントロールしたり、その旨をドキュメントにも反映させるための仕組みが必要であると考えている。