関数型プログラミングとオブジェクト指向の抜き差し可能な関係について整理して考える
Googleで適当に検索すると
とズラリと出てくる。
関数型とオブジェクト指向という一見相反するプログラミングパラダイムの併用について理解した
プログラマが知るべき97のこと/関数型プログラミングを学ぶことの重要性
新人プログラマに知っておいてもらいたい人類がオブジェクト指向を手に入れるまでの軌跡
関数型プログラミングとオブジェクト指向の抜き差しならない関係について整理して考える
とそれなりに参考になりそうな情報はあるものの、無駄に複雑化されたオブジェクト指向をストローマンにするような記事ばかり(それだけ今までのオブジェクト指向にみんなうんざりさせられているのだろう)で、そろそろきちんと自分自身「関数型プログラミングとオブジェクト指向の切り離され方」についてはっきりさせておきたい、と考え、概念整理した結論を書きます。
まず端的な結論
結論を端的に言うと、
ストリーム変換器 + 手続きの自然変換*1 ⇔ オブジェクト指向
の関係になっている。
「関数型プログラミングとオブジェクト指向を臨機応変に併用する」
だとか、
「関数型プログラミングとオブジェクト指向のマルチパラダイムである」
とすると、今まで見えていなかった部分で概念の重複が起こり、いろいろややこしいことになる、理解においても実践においても混乱を招く、実際混乱を招いている、ということになります。
関数そのものから考える
茶番はここまで。ある純粋な関数fを考えてみよう。:の左は識別子名、右は型シグネチャである。
f : A → B
fは具体的な型Aの値を受け取り、Bを返す。fは純粋なので、いつ値を渡そうと、日本の首都が鳥取になろうと、同じ値を渡せば同じ値が返ってくる。
ところが実用上は、今までに受け取った値に応じて今後の動作を変えたい場面が多々ある。パーサーやWebアプリケーションなどがその例だ(Aに文字やリクエスト、Bにデータやレスポンスが入る)。それを表現するにはどうすればよいだろうか?Bだけではなく、「次のわたし」も一緒に返せばよいのだ。
data TransAB where
TransAB : (A → (B, TransAB)) → TransAB
runTransAB : TransAB → A → (B, TransAB)
このように、入力によって出力と次の状態が決まる概念をミーリマシン(mealy machine)と呼ぶ。
「次のわたしがある」という制約によって、関数の表現力が増したのだ。
さて、HaskellやPureScriptなどの一部の言語では、手続きそのものをデータ構造として扱うことが一般的に行われている。ある程度の型の表現力があれば、手続きと、手続きの間の関数も定義できる。
もっとも簡単な手続きを定義してみよう。
data Yo x where
Yo : Yo Result
見たとおり、Yoしかないので、Yoを超えることはできない。「Yoの結果に対して演算を行う」はできず、「Yoを2回」ももちろん無理。ましてや「前のYoが成功したらYoしない」など夢のまた夢だ。
これをなんとかするために、「モナド」という概念が作られた。下のようにYoの機能を増やすと、前のYoに依存したYoが可能になる。PureとBindの導入については、モナドとはモナドであるも参照されたい。
data Yo x where
Pure : a → Yo a
Bind : Yo a → (a → Yo b) → Yo b
Yo : Yo Result
Yoを具体的な動作に変換する、Haskellに非常に近い言語による実装を示した。
runYo : ∀ x. Yo x → IO x runYo Yo = do print "Yo" return Success runYo (Pure a) = return a runYo (Bind m k) = runYo m >>= runYo . k
手続きの変換を言葉で表すと「手続きの結果が何であっても、中身の構造を保つ関数」となる。最初に扱った純粋な関数と比べると、任意の結果に対応しなければならない分、より表現力が強い。圏論ではこういった変換を自然変換(natural transformation)と呼ぶ。ただ、runYoは純粋なので、いつYoを変換しても、具体的に行われる内容は変わらない。
ここまで紹介した、2種類の関数の発展を地図に描いてみよう。
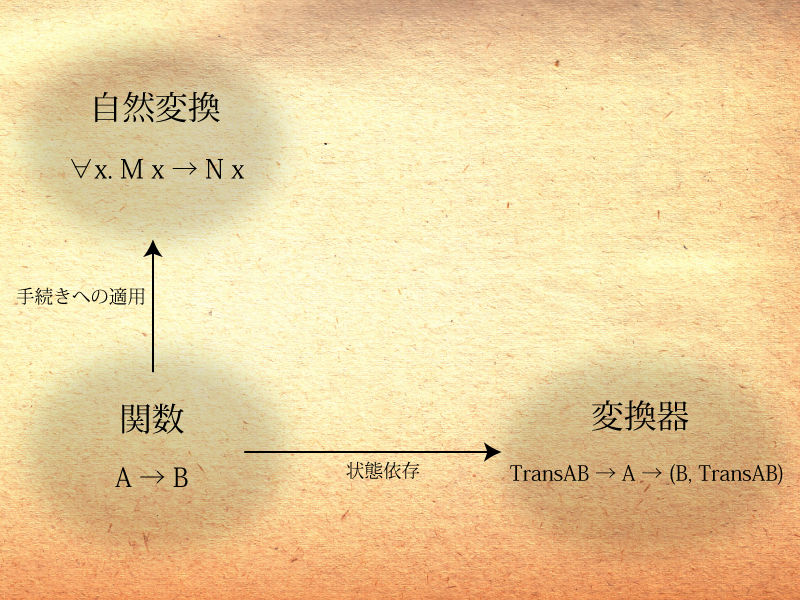
変換器を「手続きへの適用」方向に伸ばし、自然変換を「状態依存」方向に伸ばした先に宝物がある気がしてこないだろうか?
変換器の領域を緩やかに進んでいた私に、「取舵一杯」となにかが告げた。そして、突如としてそれは姿を現した(表記の統一のために一般化された代数的データ型(GADT)を用いたが、実装に必須ではない)。
data Treasure m n where
Treasure : (∀ x. m x → n (x, Treasure m n)) → Treasure m n
runTreasure : Treasure m n → m x → n (x, Treasure m n)
ある手続きを受け取ると、その結果と次の状態を返す手続きを生み出す。初めて目にするが、とてもわかりやすい、不思議な感覚。
とりあえず、ミュータブルな変数を作ってみよう。
data Identity x where
Identity : a → Identity a
data GetSet s x where
Get : GetSet s s
Set : s → GetSet s ()
variable : s → Treasure (GetSet s) Identity
variable s = Treasure (handle s)
handle :: s → GetSet s a → Identity (a, Treasure (GetSet s) Identity)
handle s Get = Identity (s, variable s)
handle s (Set s') = Identity ((), variable s')
状態を保持する能力を確認できた。次に、この概念が関数のような性質を持つか確かめてみた。まず、恒等関数相当。
echo : Functor m ⇒ Treasure m m echo = Treasure (map (λx → (x, echo)))
(Haskellの場合、mapはfmapと読み替えてほしい)
続いて、合成。$はみんな大好き関数適用演算子(f x $ g y = f x (g y))。
(>>>) : Functor n ⇒ Treasure l m → Treasure m n → Treasure l n
Treasure m >>> Treasure n = Treasure $ λe → map
(λ((x, m'), n') → (x, m' >>> n'))
(n (m e))
確かに関数のようにふるまうようだ。
この構造は私に既視感を感じさせたが、その正体がわかった。OOPにおけるオブジェクトのようにふるまうのだ。
オブジェクトは内部状態を持ち、呼ばれたメソッドに応じて、必要があれば内部状態を更新し、副作用を引き起こす――ちょうど、手続きの変換とミーリマシンの両方の性質を持っている。
result = obj.Foo(x, y)
をこのやり方で解釈すると、
(result, obj') ← runTreasure obj (Foo x y)
という表現になる。
共通する性質は、「メソッドレベルの『手続き』を、実装レベルの『手続き』に変換」しつつ、「自分の状態を更新」するという点だ。
TreasureをObjectに改名して、典型的なOOPとの対応をまとめてみよう。
| 典型的OOP | 関数型OOP |
|---|---|
| プログラム | IO型の値 |
| クラス | Object M IO型の値の定義 |
| インスタンス | Object M IO型の参照*2 |
| コンストラクタ | Object M IOを生成する関数 |
| インターフェース | M |
| メソッド | M型の値 |
| フィールド | get : M sとset : s → M ()の存在 |
| 継承 | Object M' Mとの合成 |
| オーバーライド | Object M' Mの実装の一例 |
| 菱形継承 | メソッドへのパターンマッチ |
| ダックタイピング | 存在量化 |
| カプセル化 | メソッド以外のアクセス手段なし |
| This | 不要 |
| 不可能 | IOを制限されたクラス(Object M Limited) |
| 不可能 | クラスの実装そのものへの操作((>>>t)) |
オブジェクト指向の仕組みが、たった一つの型の特殊な場合として表現できるのは、なかなか魅力的ではないだろうか。
応用
さっそく、ObjectのHaskellによる実装を作った。Object型に加え、Objectのインスタンスとして利用するためのユーティリティ関数も備えている。
現在、callというゲームエンジンへの応用を試みている。リンク先のコードのように、いかにもオブジェクト指向らしい記述を実際に可能にしている。
結論
オブジェクト指向は、関数型プログラミングと相容れない何かではなく、実装するものだ。